简明的红黑树

A Short Functional Implementation of Red Black Tree

Mar 22, 2021

见习魔法师

在处理海量数据的时候，为了快速定位到对应的数据，我们往往会用一些树结构，这些结构可以在 $O(\log{n})$ 。当然，是在最理想的情况下，如果这个二叉搜索树变得十分不平衡，例如，像链表一样，那么查询，插入，删除的时间复杂度变成了 $O(n)$ ，和在线性表内查询数据无异。为了二叉树平衡，人们发明了许多平衡二叉树，这种平衡二叉树能降低树的深度，降低时间复杂度。这些二叉树往往是通过旋转的方式来保持平衡的。你可能会在你的古老而又顽固的“数据结构”或者“算法”教科书上找到用C/C++语言实现的，长到难以理喻的又很烧脑的AVL树实现。

对于二叉搜索树而言，保持平衡是重要而又困难的事情，人们为了避免二叉搜索树成为一个大链表花了许多心思。

红黑树，作为平衡二叉树的一种，自然也十分烧脑。红黑树具有非常复杂的结构，尤其是在处理删除节点问题的时候，你可能会被复杂的分支吓到，网上也层出不穷各种“图解红黑树”的文章，虽然你可能发现他们引用的图片是同一张，然后描述各种复杂的case，最后附上一堆imperative的代码，就是那种x.y = z;的代码，不停if，赋值，然后magically得到了正确的结果。诚然红黑树十分困难，但是观看指针操作和Java的算法未动，getter setter先行的代码确实是一种煎熬。Chris Okasaki在Purely Functional Data Structures¹中提出了一种函数式的持久化的红黑树实现，整体非常简短，然而缺少了删除相关的红黑树操作；Stefan Kahrs提出了一种红黑树²，通过类型操作的方法确保算法的正确性，但是这种算法有点难以理解；Matt提出了一个简单的算法³，通过引入临时节点的方式保持红黑树的平衡性，然后再之后的平衡流程中消去红黑以外的节点来维护红黑树。这个算法非常简短，且易于理解。接下来便会介绍这个算法。

红黑树在二叉搜索树的基础上，额外将树的节点染成红黑两种颜色，特别地，叶子节点永远是黑色。红黑树采用了以下两个法则来维护搜索树的平衡：

所有红色的节点都没有红色的子节点。
从顶端（根节点）到每个叶子节点的路径都包含了相同数量的黑色节点。

这两个法则保证了从根节点到叶子节点的最长路径，不会比最短路径的两倍长，保证了树的平衡性。

接下来开始定义树的结构，因为原文使用了Standard ML，故本文也会使用ML系的语言……之一……的方言：F#。为何使用F#呢？因为可以专心于数据的转换之中，语法噪音很少。

module rec RedBlackTree
type Color =
    | Red
    | Black
type Tree<'a when 'a : comparison> =
    | Leaf
    | Branch of color : Color * left : Tree<'a> * element : 'a * right : Tree<'a>

这里需要注意的点是module rec意味着模组里的所有函数都可以相互递归。 Tree<'a when 'a: comparison>意味着树接受一个泛型参数，该类型的实例必须是可以比较的。树可以分为两类，一个是叶子节点，另一个是包含颜色，左子树，元素，右子树的分支。

首先是查找树中的元素，查找就是普通的二叉搜索树的查找方法，颜色会被忽略。

let contains x = function
    | Leaf -> false
    | Branch(_, _, y, _) when x = y -> true
    | Branch(_, left, y, right) ->
        if x < y then contains x left
        else contains x right

这个算法非常简单，如果当前节点为叶子节点，那么就没有该元素；如果当前节点的元素就是要寻找的值，就停止查找。如果要找的元素比当前元素小，就去左子树找，否则去右子树找。该算法复杂度是树高，也就是O(logn)，因为是个尾递归算法，因此会被F#编译成一个循环，非常高效。

接下来是插入算法，我们知道，一个平衡的红黑树肯定满足法则（2），既然包含了相同数量的黑色的节点，那么插入一个黑色节点势必会破坏数量的相同性质，因此只能插入红色节点。而插入红色节点可能会遇到被插入的那个节点也是红色节点的情况，这时就需要，也只需要将两个连续的红色节点平衡为一个红色的节点连接两个黑色的节点。而正因为红色的节点不会有红色的子节点，插入时该平衡操作至多执行一次。

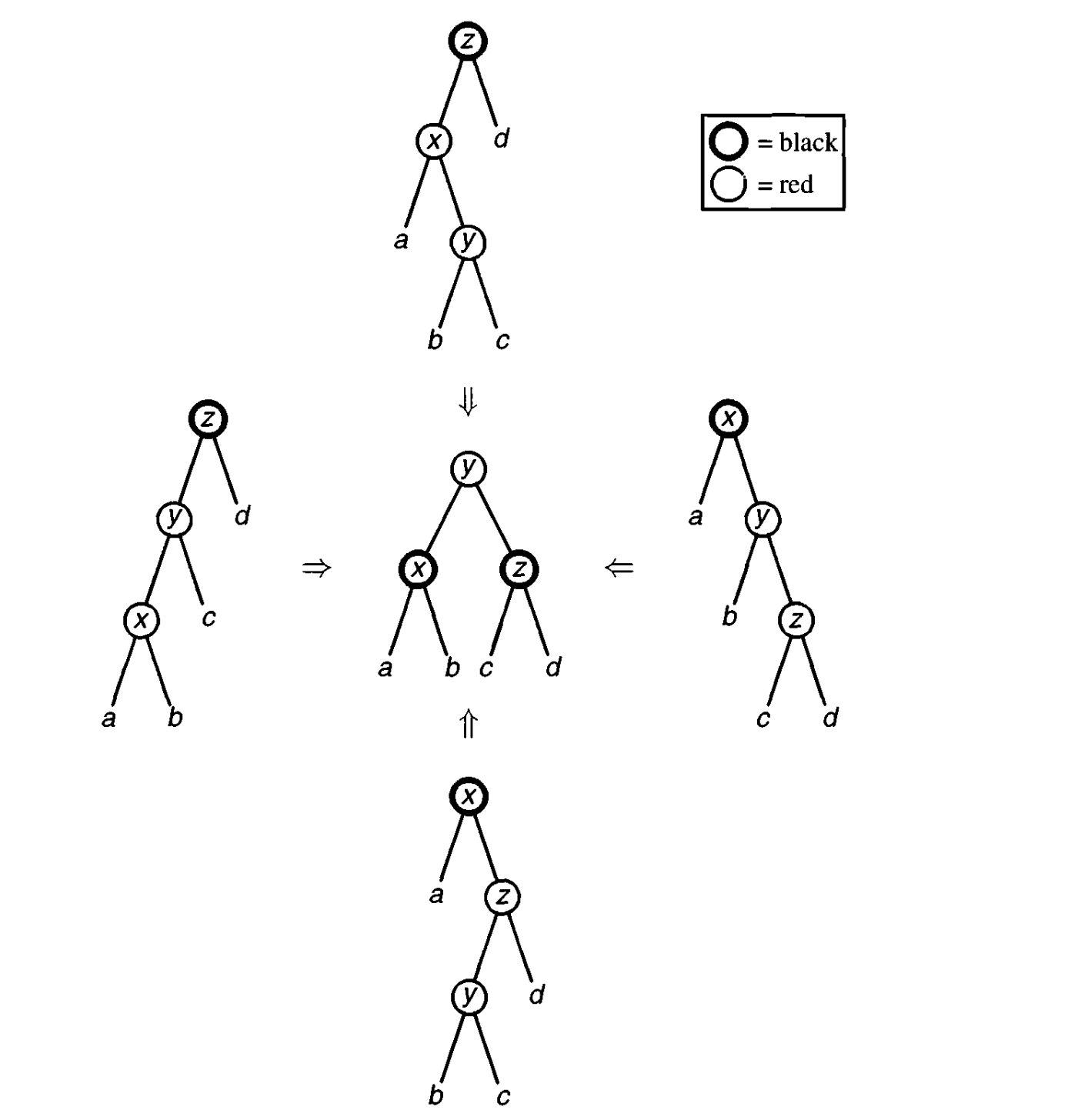
因为一个节点只有左子树和右子树两种，那么只有4种情况。

let private balance = function
    | Branch(Black, Branch(Red, a, x, Branch(Red, b, y, c)), z, d)
    | Branch(Black, Branch(Red, Branch(Red, a, x, b), y, c), z, d)
    | Branch(Black, a, x, Branch(Red, b, y, Branch(Red, c, z, d)))
    | Branch(Black, a, x, Branch(Red, Branch(Red, b, y, c), z, d)) ->
        Branch(Red, Branch(Black, a, x, b), y, Branch(Black, c, z, d))
    | tree -> tree

这个balance函数其实就是看图写话，模式匹配其中一种情况，然后将其转换为目标情况，否则就不做任何操作。

在能够balance之后，就要定义插入操作了，其实也非常方便。首先寻找到第一个需要被插入的叶子节点，将其替换为含有该元素，左右子树都是叶子的红色节点，接下来将这颗临时生成的树做平衡。平衡操作也就是解决两个相邻的红色节点的问题，在从叶子递归平衡操作直到根节点时，整棵树就平衡了。唯一需要解决的问题就是根节点此时也可能是红色的，这时其实只用将根节点的颜色染黑即可。

let insert x tree =
    let rec ins = function
        | Leaf -> Branch(Red, Leaf, x, Leaf)
        | Branch(color, left, y, right) as t ->
            if x = y then t
            else if x < y then balance(Branch(color, ins left, y, right))
            else balance(Branch(color, left, y, ins right))

    let (Branch(_, left, y, right)) = (ins tree)
    Branch(Black, left, y, right)

删除操作非常tricky，删除操作困难在删除一个黑色节点以后该如何继续保持平衡。Matt提出可以增加两种颜色，表示黑色数量为+2和-1。此时红色节点的意义就是黑色为0。同时，还需要一个表达双倍黑色的叶子节点。此时我们可以这么定义这个红黑树：

一个树被标记了一个颜色权值，最终是0和1，但是我们允许在平衡的过程中出现-1，0，1，2权的节点。在平衡结束以后这些节点不应当出现。
从根节点到叶子节点的所有简单路径的节点具有相同的权值和。
一个颜色权值为0的节点不能拥有颜色权值为0的子节点。

type Color =
    | NegBlack // 比红更红就是反黑
    | Red
    | Black
    | DoubleBlack // 比黑更黑就是二倍黑

type Tree<'a when 'a : comparison> =
    | Leaf // Its color is black
    | BlackLeaf // Its color is double black.
    | Branch of color : Color * left : Tree<'a> * element : 'a * right : Tree<'a>

然后还需要一些把颜色变红或者变黑的帮助函数：

let private redder = function
    | NegBlack | Red -> NegBlack
    | Black -> Red
    | DoubleBlack -> Black

let private blacker = function
    | NegBlack -> Red
    | Red -> Black
    | Black | DoubleBlack -> DoubleBlack

/// Make the tree black, if is a double black leaf, turn it to black.
let private blacken = function
    | Leaf | BlackLeaf -> Leaf
    | Branch (_, l, x, r) -> Branch (Black, l, x, r)

let private redderTree = function
    | Leaf | BlackLeaf -> Leaf
    | Branch(c, l, x, r) -> Branch(redder c, l, x, r)

let private blackerTree = function
    | Leaf | BlackLeaf -> BlackLeaf
    | Branch(c, l, x, r) -> Branch(blacker c, l, x, r)

let private isDoubleBlack = function
    | BlackLeaf | Branch(color = DoubleBlack) -> true
    | _ -> false

对于移除一个节点的操作而言，我们可以分为以下几种情况：

本身是叶子节点
拥有0个子节点
拥有1个子节点
拥有2个子节点

本身就是叶子节点就没啥好删除的，直接返回普通叶子节点就完事了。

在节点没有子节点的时候，就很简单了，直接删除即可。就是将其替换为一个叶子节点，为了保持颜色一致性，如果删除一个红色节点，替换为一个普通叶子节点；否则替换为一个二倍黑色叶子节点。

如果一个节点只有叶子节点，那么它一定是一个黑色节点，而且它的唯一的子节点一定是红色的。理由十分简单：

如果一个红色节点只有一个子节点，那么为了满足性质（2），即所有路径包含相同数量的黑色节点，因为另外的节点是叶子，所以另外一个节点只能是红色的，而这又违反了性质（1），故红色节点不可能只有一个子节点。
如果一个黑色节点拥有唯一一个黑色节点，那么从该节点出发，左右到达叶子节点的简单路径一定无法包含相同数量的黑色节点。

因此只有唯一的情况，即黑色节点拥有红色节点。

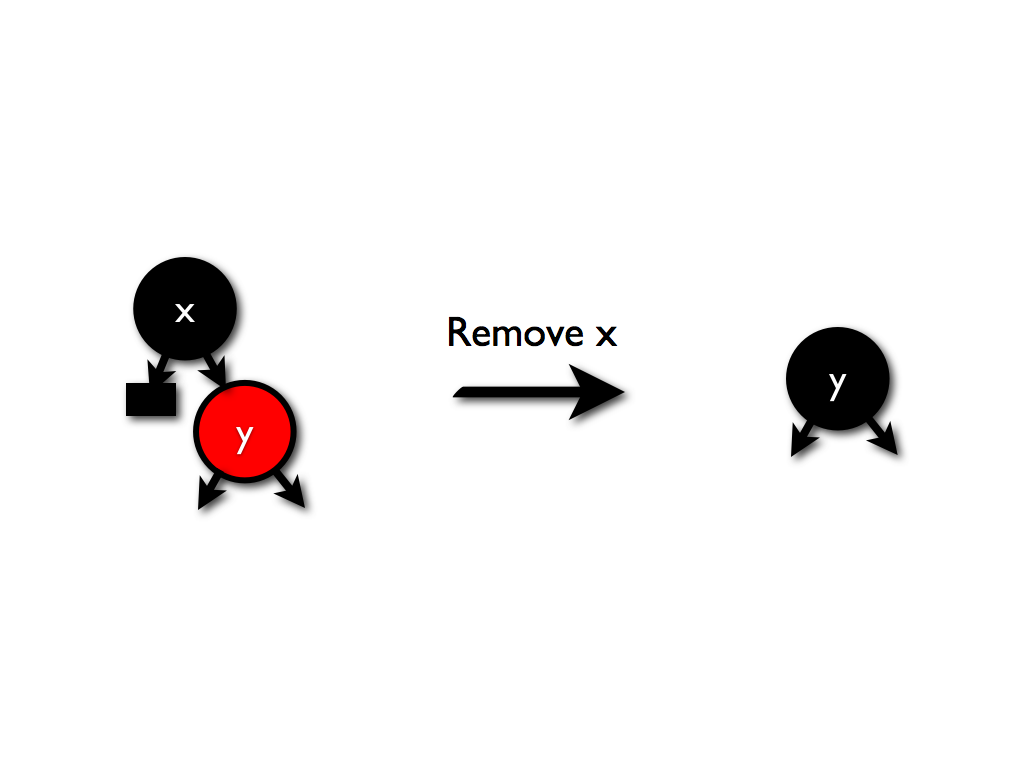
这种情况非常简单，只用将其唯一的子节点替换当前节点，然后把他染黑就行了。

那么如果一个节点拥有两个子节点呢？那么只用把这个节点的左节点的最右节点（即最大值）的值替换当前节点，然后把那个最大值节点删除即可。这样可以保证性质（2）还是满足的，因为我们相当于删除了左树中的最大值的那个节点，而删除操作我们保证了保持平衡（虽然我们现在正在删除的过程中），但是递归只要每个情况都满足这个性质，那么最终的过程肯定也满足。

let max = function
    | Branch(_, _, x, Leaf) -> x
    | Branch(_, _, _, right) -> max right
    | _ -> invalidOp "max of leaf"

let removeMax = function
    | Branch(color, left, elem, Leaf) ->
        remove(Branch(color, left, elem, Leaf))
    | Branch(color, left, elem, right) ->
        bubble(Branch(color, left, elem, removeMax right))
    | _ -> invalidOp "remove max of leaf"

let remove = function
    | Leaf | BlackLeaf -> Leaf
    | Branch(Red, Leaf, _, Leaf) -> Leaf
    | Branch(Black, Leaf, _, Leaf) -> BlackLeaf
    | Branch(Black, Leaf, _, Branch(Red, a, x, b))
    | Branch(Black, Branch(Red, a, x, b), _, Leaf) ->
        Branch(Black, a, x, b)
    | Branch(color, left, _, right) ->
        let maxVal = max left
        let removedLeft = removeMax left
        bubble(Branch(color, removedLeft, maxVal, right))

现在我们成功删除了节点，而且同时保持了从根节点到每个叶子节点拥有相同数量的颜色权值和。但是我们是以添加了奇怪的中间节点为代价的，因此下一步我们应当重新平衡，消去这些颜色。

删除这些颜色可以分为冒泡——重平衡两个步骤；前者负责将子节点的颜色“提升”到父节点，即如果某个节点存在一个颜色权值为2的节点，则将该节点的颜色提升，具体做法是把两个子节点权值减少，然后把父节点的颜色增加。这样虽然可能会出现-1，2的节点，但是在最后平衡的过程中我们可以消去。

let private bubble = function
    | Branch(color, left, elem, right) when isDoubleBlack left || isDoubleBlack right ->
        balance(Branch(blacker color, redderTree left, elem, redderTree right))
    | tree -> balance tree

当然，目前写的balance函数不够了，需要handle父节点为双倍黑的情况。

在之前的balance函数里，我们已经能够处理这些情况了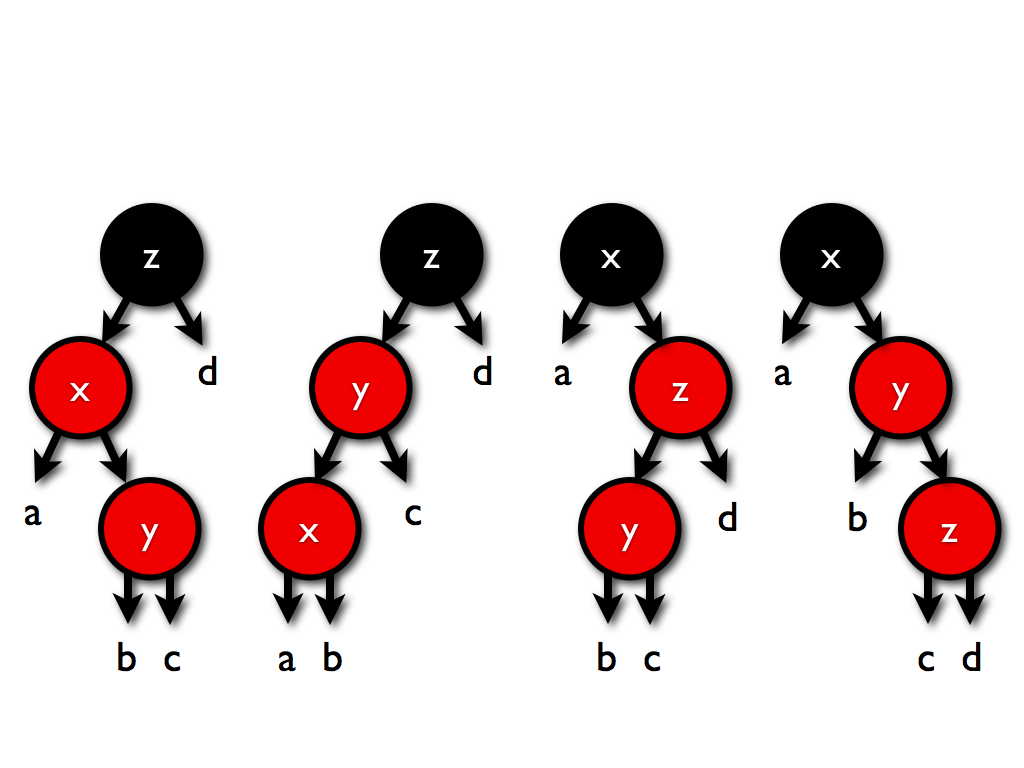：这些会被转换成：

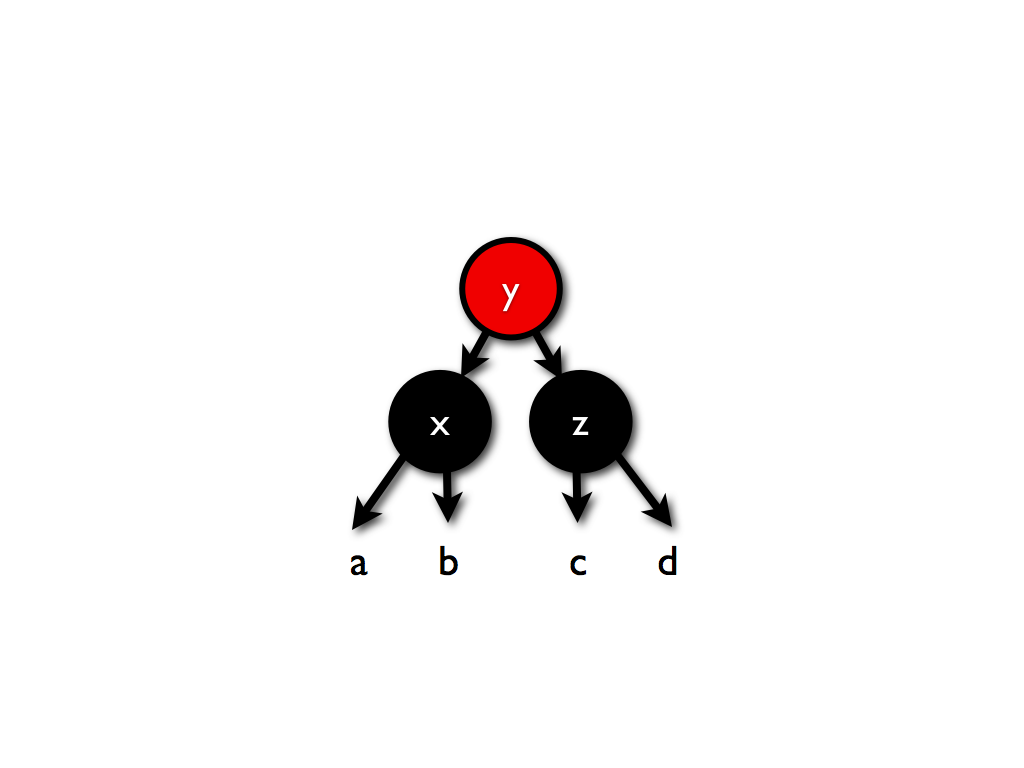
如果父节点是两倍黑色呢？

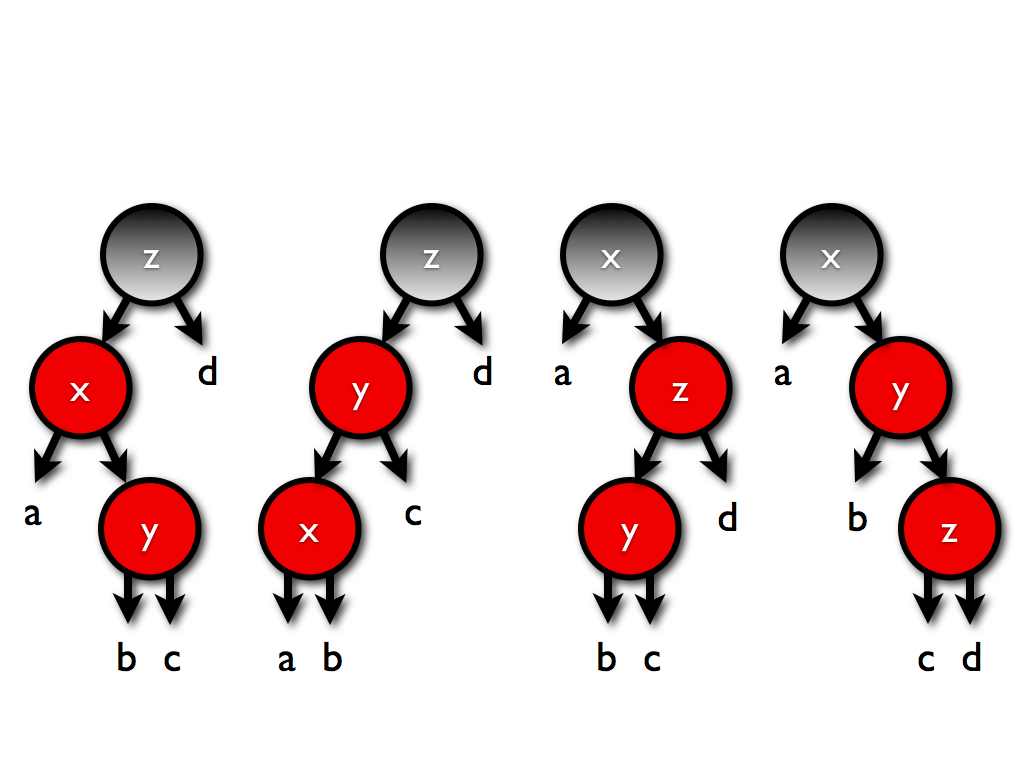
那么变换后的其实没有区别，除了变换后的根节点是黑色的（为了保持颜色权值和不变）。

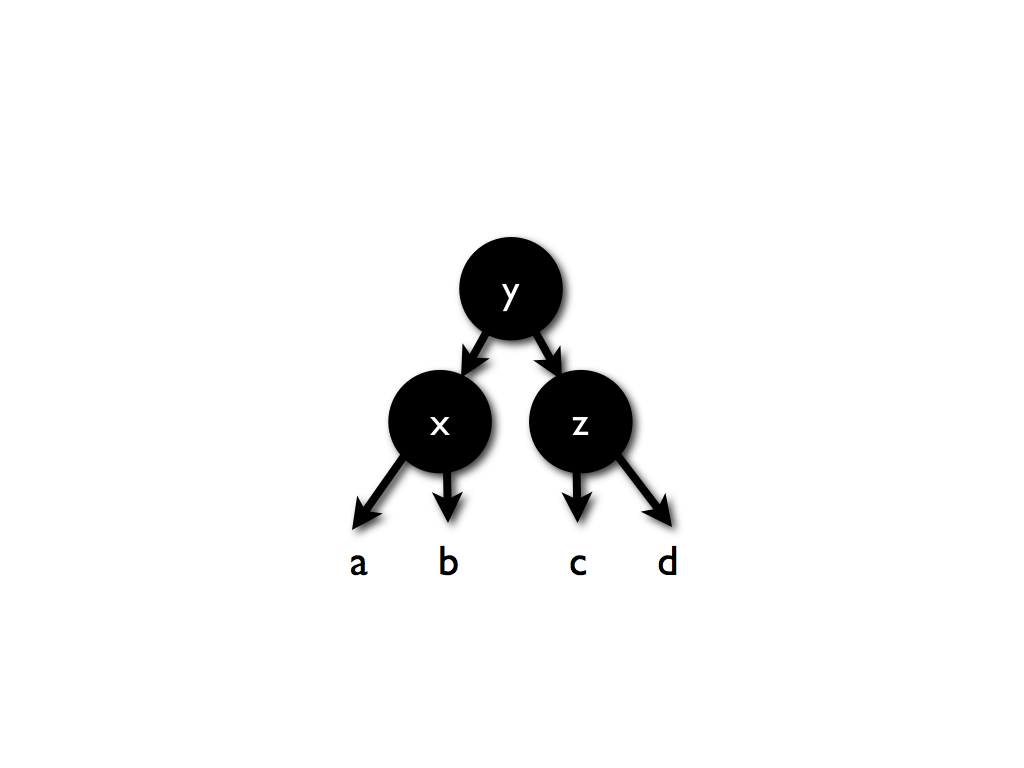
那么我们可以发现，虽然颜色不同，但是只是让根节点颜色变淡罢了，因此可以这么改写情况，让他适应新的case：

let private balance = function
    | Branch(Black | DoubleBlack as color, Branch(Red, a, x, Branch(Red, b, y, c)), z, d)
    | Branch(Black | DoubleBlack as color, Branch(Red, Branch(Red, a, x, b), y, c), z, d)
    | Branch(Black | DoubleBlack as color, a, x, Branch(Red, b, y, Branch(Red, c, z, d)))
    | Branch(Black | DoubleBlack as color, a, x, Branch(Red, Branch(Red, b, y, c), z, d)) ->
        Branch(redder color, Branch(Black, a, x, b), y, Branch(Black, c, z, d))

最后只需处理颜色权值为-1的节点，如果出现颜色为-1的节点，那么其父节点一定是二倍色的，并且其子节点一定是黑色的。原因很简单：

反黑色节点智慧在冒泡阶段出现，冒泡执行的时机是当某个节点拥有一个二倍黑的节点时，将这节点的两个节点的颜色都变得更红，此时如果某个节点是红色，则该节点变成-1的颜色。那么因为该节点拥有红色的子节点，该节点一定是黑色的，所以它会变成二倍黑；因为它曾是红色节点，因此它的两个子节点一定是黑色。

所以情况就是这样：

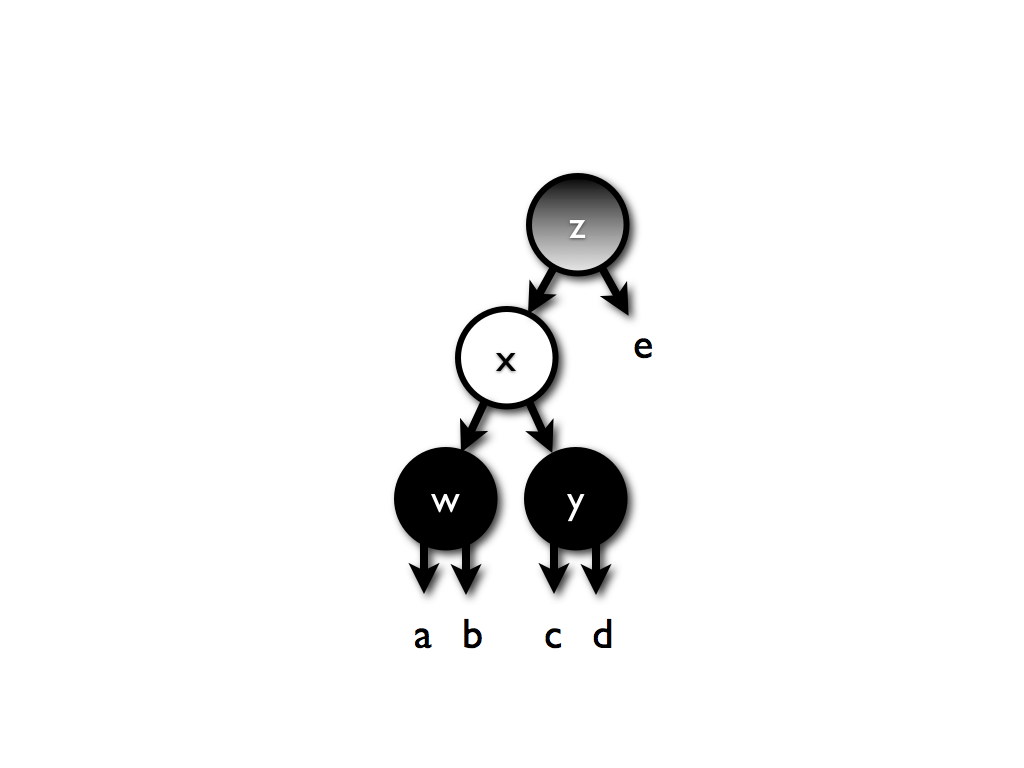
这个会变成：

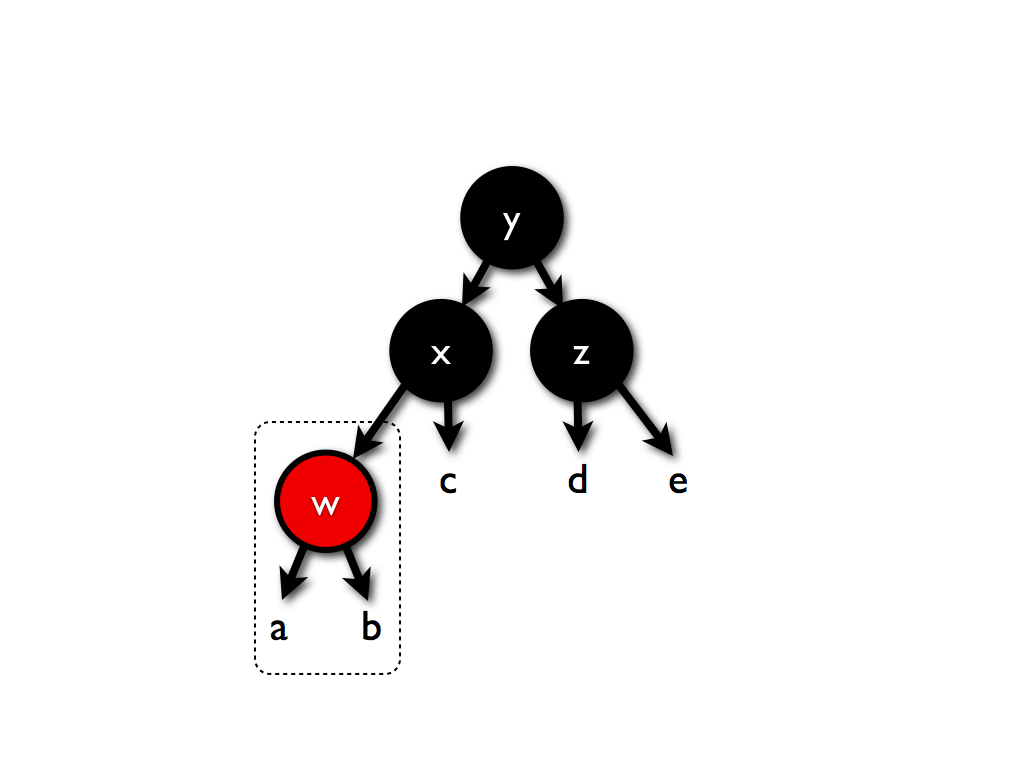
因为无法确定a以及b节点的颜色，因此这里可能会出现两个连续的红色节点，因此w这棵树需要重新平衡。

平衡的代码只需多两个case即可（分别是对称的情况）：

let private balance = function
    | Branch(Black | DoubleBlack as color, Branch(Red, a, x, Branch(Red, b, y, c)), z, d)
    | Branch(Black | DoubleBlack as color, Branch(Red, Branch(Red, a, x, b), y, c), z, d)
    | Branch(Black | DoubleBlack as color, a, x, Branch(Red, b, y, Branch(Red, c, z, d)))
    | Branch(Black | DoubleBlack as color, a, x, Branch(Red, Branch(Red, b, y, c), z, d)) ->
        Branch(redder color, Branch(Black, a, x, b), y, Branch(Black, c, z, d))
    | Branch(DoubleBlack, a, x, Branch(NegBlack, Branch(Black, b, y, c), z, Branch(Black, d, e, f))) ->
        Branch(Black, Branch(Black, a, x, b), y, balance(Branch(Black, c, z, Branch(Red, d, e, f))))
    | Branch(DoubleBlack, Branch(NegBlack, (Branch(color = Black) as tree), x, Branch(Black, b, y, c)), z, d) ->
        Branch(Black, balance(Branch(Black, redderTree tree, x, b)), y, Branch(Black, c, z, d))
    | tree -> tree

那么寻找某个值并删除也就写完了，主要的过程和插入完全相同。

let delete x tree =
    let rec rem = function
        | Leaf | BlackLeaf -> Leaf
        | Branch(color, left, y, right) as t ->
            if x = y then remove t
            else if x < y then bubble(Branch(color, rem left, y, right))
            else bubble(Branch(color, left, y, rem right))

    blacken (rem tree)

最后因为经过了平衡操作，所以我们还是要把根节点染黑。

经过了百行左右的代码，你已经写完了红黑树了。可能这篇文章还没有某些红黑树的Java实现长，完整的代码可以在这个Gist里找到。

当然一开始也有个Lisa实现的红黑树，但是考虑到受众可能不会lisa，所以我们采用了F#，采用完全声明式的代码能增加可读性。Lisa版的实现在这个Gist里可以找到。

r{{ changeThemeOnce({ primary: '#FB5458', secondary: 'black' }) }} r{{ changeExtraDisplaySettings({blurMainImage: true}) }}

Okasaki, C. (1998). Some Familiar Data Structures in a Functional Setting. In Purely Functional Data Structures (pp. 17-30). Cambridge: Cambridge University Press. doi:10.1017/CBO9780511530104.004 ↩
Kahrs, S. (2001) “Red-black trees with types”, Journal of Functional Programming. Cambridge University Press, pp. 425-432. doi: 10.1017/S0956796801004026. ↩
The missing method: Deleting from Okasaki's red-black trees ↩