在某知名(hu)网站中,写一个语言的解析器似乎是一个计算机学生的基本功,那么如果非要写一个玩具语言,什么语言比较好呢?自然是lisp,因为其基于S Expression,而他的语法产生式又无比简单。
String -> S Expression
针对这个结构,我们就能定义出S Expression的代数数据结构:
sealed trait SimpleLispTree
case class Value(get: String) extends SimpleLispTree
case class SList(list: Seq[SimpleLispTree]) extends SimpleLispTree
其中,对表达式生成树的解析可以通过NaïveJSON实现,其代码如下:
def sAtom = "[^() \\s]+".r map Value
def sExpression: Parser[SimpleLispTree] =
("(" *> many(sExpression) <* ")" map SList) | sAtom
没错,就是那么一点,而且几乎就是生成式的直译。
S Expression -> AST
然后我们就要根据Lisp树生成抽象语法树(AST),首先我们定义基本的数据类型。
sealed trait Expression
case class Symbol(value: String) extends Expression
case class SInteger(value: Int) extends Expression
case class SBool(value: Boolean) extends Expression
case object NilObj extends Expression
然后定义两个最基本的操作,Apply和Define,分别代表调用一个函数和定义一个变量或函数。
case class Apply(head: Expression, args: List[Expression]) extends Expression
case class Define(symbol: Symbol, value: Expression) extends Expression
和 (if <predicate> <consequence> <alternative>) 的if语句:
case class SIfElse(predicate: Expression, consequence: Expression, alternative: Expression) extends Expression
之后便是如何定义函数了,我们有些东西必须是内置的,在这里是指用Scala写的函数,那么为了互操作,便有了某种代表基本函数的类型。 因为我们不知道参数的个数,所以传入一个表达式的列表,返回一个表达式。
case class PrimitiveFunction(function: List[Expression] => Expression) extends Expression
case class LambdaExpression(body: Expression, boundVariable: List[Symbol]) extends Expression
case class Closure(boundVariable: List[Symbol], body: Expression, capturedEnv: Environment) extends Expression
别忘了有一个表达毛都没有的表达式:
case class Failure(tp: String, message: String) extends Expression
好了,这就是所有的数据结构了,如果想要扩充,比如增加一个String,就可以在Expression类上扩充了。同时如果你想在解析的层面增加,比如增加quote的语法糖,就可以在parser和SimpleLispTree上扩充。
如何生成AST呢?如何编写一个compile函数?他本身的架构其实十分明晰,是一个很长的case分析,对于不同的S树生成AST树,所以他应该长这个样:
def compile(tree: SimpleLispTree): Expression = tree match {
case ... => ???
}
首先最简单的是true和false,如果碰到true直接生成对应的SBool(true)就行。
case Value("true") => SBool(true)
case Value("false") => SBool(false)
如果他长得像数字,那就是数字,否则他可能是要引用一个符号。
case Value(value) => {
if(value.matches("-?\\d+")) SInteger(value.toInt)
else Symbol(value)
}
这是我们碰到单个原子的所有情况,接下来就是形如(A B C ...) 的情况了。
case SList(ls) => ls match {
case ??? => ???
}
接下来我们填充这个subcase里面的内容
if 的情况最简单,如果这个list是if开头,而且紧跟着三个树,即形如(if A B C),那么就分别将这三个生成AST,然后填入SIfElse的结构中。如果不满足,就报错。
case Value("if")::xs => xs match {
case pred :: cons :: alt :: Nil =>
SIfElse(compile(pred), compile(cons), compile(alt))
case _ => Failure("Syntax Error", "If else expect three expressions.")
}
然后是define,其实就是(define A B) ==> Define(A, compile(B))
case Value("define")::xs => xs match {
case Value(sym)::expr::Nil => Define(Symbol(sym), compile(expr))
case _ => Failure("Syntax Error", "Cannot define a variable like that.")
}
(define (f x) x) <=> (define f (lambda (x) x))的话,你可以在中间加上这么一句:
case SList(Value(sym)::params)::sExpr =>
Define(Symbol(sym), LambdaExpression(compile(sExpr), params.map(compile(_).asInstanceOf[Symbol])))
接下来就是lambda表达式的解析:
case Value("lambda" | "λ")::xs => xs match {
case SList(params)::sExpr::Nil =>
LambdaExpression(compile(sExpr), params.map(compile(_).asInstanceOf[Symbol]))
case _ => Failure("Syntax Error", "Error creating a lambda expression.")
}
压轴的也是最重要的,就是形如(A B)的解析,应用(Application)的解析也十分简单:
case head::tail => Apply(compile(head), tail.map(compile))
case Nil => NilObj
AST, Env -> Expression, Env
如果你恰巧也看过SICP,那么元循环求值器一定会给你留下深刻的印象,但是那个是让lisp解析lisp,所以生成语法树的部分都可以省去不写,没错,到现在我们才开始写eval和apply。
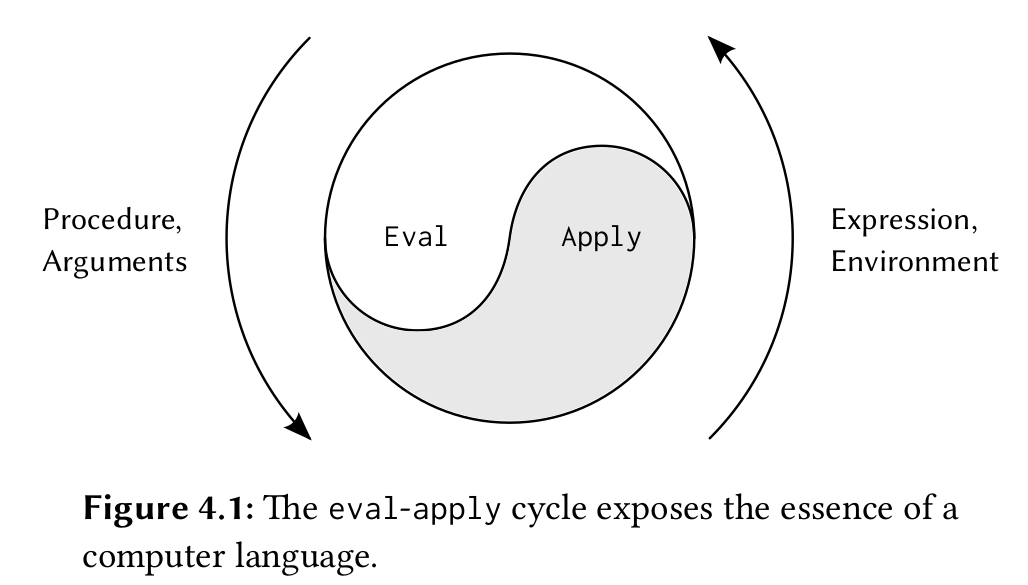
eval 是传入表达式和环境,生成结果表达式和新的环境的函数。 apply是传入lambda表达式和参数,返回lambda应用到参数的结果。
等等,什么是环境?
环境的定义可以参考environment,其本质就是一个拥有多个符号和表达式一一对应的列表,同时也有一个父环境,如果子环境找不到值,就往父环境上找。
如图,
 factorial里面的n为什么互不影响,是因为这些n都在不同的环境里。
factorial里面的n为什么互不影响,是因为这些n都在不同的环境里。
根据定义,写出代码
sealed trait Environment {
def has(key: String): Boolean
def getValueOption(key: String): Option[Expression]
def newFrame = Env(Map.empty, this)
def withValue(key: String, value: Expression): Env = newFrame withValue (key, value)
def withValues(context: Seq[(String, Expression)]): Env = newFrame withValues context
}
case class Env(env: Map[String, Expression], parent: Environment) extends Environment {
override def has(key: String): Boolean = env.contains(key) || parent.has(key)
override def getValueOption(key: String): Option[Expression] =
env.get(key).orElse(parent getValueOption key)
override def withValue(key: String, value: Expression): Env = copy(env + (key -> value))
override def withValues(context: Seq[(String, Expression)]): Env = copy(env ++ context)
}
object EmptyEnv extends Environment {
override def has(key: String): Boolean = false
override def getValueOption(key: String): Option[Expression] = None
}
如何定义eval的结果呢,自然需要一个新的代数数据类型。
trait EvalResult {
def flatMap(fn: Expression => EvalResult): EvalResult
def flatMapWithEnv(fn: (Expression, Environment) => EvalResult): EvalResult
def isSuccess: Boolean
}
case class EvalSuccess(expression: Expression, env: Environment) extends EvalResult {
override def flatMap(fn: Expression => EvalResult): EvalResult = fn(expression)
override def flatMapWithEnv(fn: (Expression, Environment) => EvalResult): EvalResult =
fn(expression, env)
override def isSuccess: Boolean = true
}
case class EvalFailure(message: String) extends EvalResult {
override def flatMap(fn: Expression => EvalResult): EvalResult = this
override def flatMapWithEnv(fn: (Expression, Environment) => EvalResult): EvalResult = this
override def isSuccess: Boolean = false
}
好的,接下来才是正题了
eval
eval的整体架构和compile类似,本质是一个pattern matching。
def eval(exp: Expression, env: Environment): EvalResult = {
def pureValue(expression: Expression) = EvalSuccess(expression, env)
def unit(newEnv: Environment) = EvalSuccess(NilObj, newEnv)
exp match {
case ??? => ???
}
}
pureValue和unit都是帮助函数。
- pureVale代表目前的操作没有副作用,无法对环境造成影响。
- unit代表目前的操作对环境产生了影响,因此返回一个Nil。
首先是一些在compile阶段就求值完毕的值,碰到他们直接返回他们本身就可以。
case f: Failure => pureValue(f)
case bool: SBool => pureValue(bool)
case NilObj => pureValue(NilObj)
case c: Closure => pureValue(c)
case fn: PrimitiveFunction => pureValue(fn)
case i: SInteger => pureValue(i)
接下来是符号,如果碰到符号,就在环境中寻找对应的值,如果找不到就报错。
case Symbol(sym) => env.getValueOption(sym).map(pureValue).getOrElse(EvalFailure(s"Symbol $sym not found."))
如果遇到lambda表达式,就生成一个闭包,捕获当前环境。
case LambdaExpression(body, boundVariable) =>
pureValue(Closure(boundVariable, body, env))
为何要捕获当前环境?
此处涉及到动态作用域和静态作用域的区别。
-
动态作用域:函数运行的上下文取决于当前的环境,类似于emacs-lisp,这样的好处是解释器的实现十分简单,如果要实现动态作用域,在eval的时候如果碰见lambda表达式就直接返回,然后再直接在eval的上下文中执行lambda表达式的body即可。但是,几乎所有的语言都采用了静态作用域,因为动态作用域能带来一些意想不到的麻烦。
-
静态作用域(词法作用域):函数所使用的自由变量仅仅取决于函数定义的位置。
采用静态作用域的好处是显著的,因为你无需担心一个变量的改变会影响某一个函数的执行。
(define x 0)
(define (f y) (+ x y))
(f 2)会返回2,正如我们期待的那样,而且我们也想让这个函数无论在哪里被调用,行为都是一致的。否则,你需要递归查看每一个函数到底有没有使用什么自由变量。
(define (hello)
(define x 1)
(f 2)
)
如果是动态作用域,此处应该返回3。这显然会引入意想不到的错误。例如NaiveExpr的作用域就是动态的,而且只有一种作用域,函数也没有绑定变量,只有自由变量。所谓的函数调用也只是临时限定了上下文,不能像栈一样隐藏(shadow)在递归调用时的不同局部变量。因此无法递归。但是NaiveExpr这么设计是因为课程设计的要求就是这样……并没有什么办法。
静态作用域在此处的实现有一个小坑,就是闭包在创建的时候无法捕获包含自己的环境。因为在定义的时候,闭包还没有创建完成。因此大多数语言对递归的事物都有特殊的实现,比如F#就区分let和let rec。当然其中的一种思路就是使用可变状态,在闭包捕获某个可变环境之后,再将环境中的对应闭包修改为捕获自身的闭包。这个我们之后再说。
如果遇到define,那么就计算define的value,再生成新的环境,把define的symbol绑定到value的eval结果上。
case Define(Symbol(sym), expr) => eval(expr, env) flatMap {
result => unit(env.withValue(sym, result))
}
如果遇到函数调用,就先计算参数,再将参数应用到过程上。
case Apply(func, args) => eval(func, env) flatMap {
proc => evalList(args, env).fold(EvalFailure,
evaledArguments => apply(proc, evaledArguments.toList).fold(EvalFailure, EvalSuccess(_, env)))
}
如果遇到if,那么先计算第一个predicate,然后根据其真假,选择eval第二个还是三个参数。
case SIfElse(predicate, consequence, alternative) =>
eval(predicate, env) flatMap {
case SBool(b) => eval(if(b) consequence else alternative, env)
case other => EvalFailure(s"Unexpected if predicate value: $other")
}
eval整体就是那么多
apply
接下来是apply,apply本质上是根据闭包捕获的环境,配上其参数,将其组合成一个新的环境,然后在新的环境中eval闭包的body。
def apply(procedure: Expression, arguments: List[Expression]): Either[String, Expression] =
procedure match {
case Closure(boundVariable, body, capturedEnv) => {
if (boundVariable.length != arguments.length)
Left(s"Function expected ${boundVariable.length} args but ${arguments.length} found.")
else
eval(body, capturedEnv.newFrame.withValues(boundVariable.map(_.value).zip(arguments))) match {
case EvalSuccess(result, _) => Right(result)
case EvalFailure(msg) => Left(msg)
}
}
case PrimitiveFunction(fn) =>
Try(fn(arguments)).fold(ex => Left(ex.getLocalizedMessage), Right(_))
case _ => Left(s"Cannot apply $procedure to $arguments.")
}
从这里可以看到,eval和apply是相辅相成的,apply本质是一个eval,eval又需要apply来实现。
evlist
接下来剩下一个没有介绍的evalList了我们要实现的是获取一个表达式的列表和环境,生成在这个环境中将列表每个表达式分别求值后的结果。
def evalList(exps: Seq[Expression], env: Environment): Either[String, Seq[Expression]] = {
val evaledExpr = exps.map(eval(_, env))
if(evaledExpr.forall(_.isSuccess))
Right(evaledExpr.map(_.asInstanceOf[EvalSuccess].expression))
else Left(evaledExpr.find(!_.isSuccess).get.asInstanceOf[EvalFailure].message)
}
别急,其实还有坑
你以为这就结束了?不! 如果就这么按部就班地写,到最后,你会发现,函数是无法递归的,因为在生成闭包的时候,捕获环境时是无法捕获自身的。 当然,你可以用Y-组合子:
(define (Y fn) ((lambda (u) (u u)) (lambda (f) (fn (lambda (s) ((f f) s))))))
但是,如果一个函数式语言不能递归,和废物有什么区别呢?有一个解决方法就是引入局部可变状态,使得在引入这个函数后再改变函数捕获的环境。不要担心,因为可控的局部可变状态不会影响引用透明性。同时别的无副作用方法都不是十分优雅。
实现递归
这里有一个简单的实现递归的例子。 我们扩充Environment:
case class MutableEnv(private val env: collection.mutable.Map[String, Expression],
parent: Environment) extends Environment {
override def has(key: String): Boolean = env.contains(key) || parent.has(key)
override def getValueOption(key: String): Option[Expression] =
env.get(key).orElse(parent getValueOption key)
def addValue(key: String, value: Expression): MutableEnv = {
env.update(key, value)
this
}
}
然后修改eval的define分支,增加一个判断:
case closure@Closure(_, _, capturedEnv, _)
val recursiveFrame = MutableEnv(collection.mutable.Map.empty, capturedEnv)
val recursiveClosure = closure.copy(capturedEnv=recursiveFrame)
recursiveFrame.addValue(sym, recursiveClosure)
unit(env.withValue(sym, recursiveClosure))
这样,就以一种简单的方式实现了递归。可见,不需要教条般信仰不可变状态,在合适的时候用合适的工具才是重要的。
Test Cases
实现一个元组:
(define cons
(lambda (x y)
(lambda (m) (m x y))))
(define car (lambda (m) (m (lambda (a b) a))))
(define cdr (lambda (m) (m (lambda (a b) b))))
下一步?
为了使你的语言不那么像玩具(其实就是),可以扩充一下文法,或者编写系统函数,使得在执行环境中能被调用。
但是别慌,还有一个大坑等着你们填:如何实现注释?(逃
还比如说,在参数层面上实现模式匹配(你猜猜怎么实现多态函数):
(define (fact 0) 1)
(define (fact n)
(* n (fact (- n 1))))
实现玩具语言,虽然有点累人,但是还是十分有趣的(确信)。
r{{ changeExtraDisplaySettings({metaBelowImage: true}) }}
